
Winner's Guide Volume 3: Full Pay Deuces Wild
by Bob Dancer
From the authors of the best-selling video poker strategy cards, the Video Poker Winner's Guides cover both strategy and non-strategy aspects of play that are important for winning. Choose among four levels of strategy, via the presentation and explanation of basic principles. Strategies for full-pay as well as the more widely available non-full-pay versions are covered. These reports present the most complete and accurate strategies available for these games.
Read a review of Winner's Guide Volume 3: Full Pay Deuces WildIncrease Your Deuces Wild Odds!
The Deuces Wild video poker game at All Slots Casino has a 96.77% return with five coins in. You can play in denominations from $.05 to $5.00 and the machine gives you hints on what to hold for obvious hands, but you'll still need your strategy cards or your rules memorized to get the biggest payback. The graphics and design are well-done.
A Flush vs. Straight Paradox in Deuces Wild
by Bob Dancer
You're playing some version of Deuces Wild and are dealt 5 6
6 7
7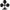 8
8 K
K . Your choice is between the unsuited 5678 or the suited 568K. Which is better?
. Your choice is between the unsuited 5678 or the suited 568K. Which is better?
 6
6 7
7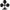 8
8 K
K . Your choice is between the unsuited 5678 or the suited 568K. Which is better?
. Your choice is between the unsuited 5678 or the suited 568K. Which is better?If you go for the straight, there are 12 good Bob Dancer is one of the world's foremost video poker experts. He is a regular columnist for Casino Player, Strictly Slots, and the Las Vegas Review-Journa land has written an autobiography and a novel about gambling. He provides advice for tens of thousands of casino enthusiasts looking to play video poker. Bob's website is www.bobdancer.com cards in the deck. Four 4s, four 9s, and four deuces. If you are going for the flush, there are also 12 good cards in the deck. Four deuces and eight hearts --- remembering not to count the 2
Bob Dancer is one of the world's foremost video poker experts. He is a regular columnist for Casino Player, Strictly Slots, and the Las Vegas Review-Journa land has written an autobiography and a novel about gambling. He provides advice for tens of thousands of casino enthusiasts looking to play video poker. Bob's website is www.bobdancer.com cards in the deck. Four 4s, four 9s, and four deuces. If you are going for the flush, there are also 12 good cards in the deck. Four deuces and eight hearts --- remembering not to count the 2 twice. Twelve good cards one way. Twelve good cards the other. It's a tie. Right?
twice. Twelve good cards one way. Twelve good cards the other. It's a tie. Right?
 Bob Dancer is one of the world's foremost video poker experts. He is a regular columnist for Casino Player, Strictly Slots, and the Las Vegas Review-Journa land has written an autobiography and a novel about gambling. He provides advice for tens of thousands of casino enthusiasts looking to play video poker. Bob's website is www.bobdancer.com cards in the deck. Four 4s, four 9s, and four deuces. If you are going for the flush, there are also 12 good cards in the deck. Four deuces and eight hearts --- remembering not to count the 2
Bob Dancer is one of the world's foremost video poker experts. He is a regular columnist for Casino Player, Strictly Slots, and the Las Vegas Review-Journa land has written an autobiography and a novel about gambling. He provides advice for tens of thousands of casino enthusiasts looking to play video poker. Bob's website is www.bobdancer.com cards in the deck. Four 4s, four 9s, and four deuces. If you are going for the flush, there are also 12 good cards in the deck. Four deuces and eight hearts --- remembering not to count the 2 twice. Twelve good cards one way. Twelve good cards the other. It's a tie. Right?
twice. Twelve good cards one way. Twelve good cards the other. It's a tie. Right?Maybe. If flushes and straights pay the same amount, as they do in many versions of Deuces Wild, then yes, it's a tie. With many other Deuces Wild pay schedules, however, flushes pay more than straights. If 5-coin flushes pay 15 and 5-coin straights pay only 10, then of course 12 chances at getting 15 is worth 50% more than 12 chances at getting 10.
Now let's add a deuce (signified by a W, standing for wild card) to the mix and see what changes. In NSU Deuces Wild (a 99.73% game with a single-coin pay schedule including 16-10-4-4-3-2-1), flushes (signified by the 3 in the pay schedule) pay 50% more than a straight (signified by the 2). On a hand such as W 7 8
8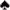 9
9 Q
Q , it is correct to hold W789 and try for the straight. On a hand such as W 3
, it is correct to hold W789 and try for the straight. On a hand such as W 3 6
6 9
9 Q
Q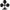 , it is correct to only hold the deuce.
, it is correct to only hold the deuce.
 8
8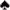 9
9 Q
Q , it is correct to hold W789 and try for the straight. On a hand such as W 3
, it is correct to hold W789 and try for the straight. On a hand such as W 3 6
6 9
9 Q
Q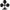 , it is correct to only hold the deuce.
, it is correct to only hold the deuce.This is strange. Straights aren't worth as much as flushes and yet it's correct to try for the straight and not try for the flush. What gives?
Holding a 1-deuce 4-card open-ended straight is one of the few hands in Deuces Wild where your expectation is to exactly get your money back. This is true for every pay schedule that yields even money for 3-of-a-kinds and double your money for straights --- which means almost every Deuces Wild pay schedule. Of the 47 possible draws, there are 9 cards that will give you your money back, 19 that will create a straight, and 19 that will give you zero. Since you get double your money on the straights, this exactly offsets the equal number of times you strike out. If you are drawing to W789 for example, there are four each of 5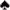 , 6
, 6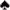 , T
, T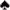 , and J
, and J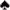 , plus the three other deuces yielding 19 straights. The 9 cards that yield 3-of-a-kinds are the remaining three 7s, 8s, and 9s. There are 19 cards not mentioned, and these yield no score at all.
, plus the three other deuces yielding 19 straights. The 9 cards that yield 3-of-a-kinds are the remaining three 7s, 8s, and 9s. There are 19 cards not mentioned, and these yield no score at all.
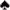 , 6
, 6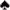 , T
, T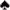 , and J
, and J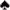 , plus the three other deuces yielding 19 straights. The 9 cards that yield 3-of-a-kinds are the remaining three 7s, 8s, and 9s. There are 19 cards not mentioned, and these yield no score at all.
, plus the three other deuces yielding 19 straights. The 9 cards that yield 3-of-a-kinds are the remaining three 7s, 8s, and 9s. There are 19 cards not mentioned, and these yield no score at all.Knowing that you get even money for holding the 4-card straight doesn't give you enough information to tell you whether it's the right play or not. You also need to know how much holding a single deuce is worth. If it is worth MORE than even money (which is often true), then you should hold just the deuce. If it is worth LESS than even money (which is true sometimes), then you should hold the straight. Figuring this out is not trivial. For every hand there are 178,365 different combinations of cards you can draw to a single deuce. And each of these must be multiplied by the pay schedule to determine the value of holding the deuce. And exactly how many straights, flushes, straight flushes, wild royals, etc., varies depending on exactly which three cards combine with the deuce to make up the straight (and whether any of these three cards are suited with each other), and even what the fifth card is (and whether the fifth card is or is not suited with one of the cards making up the straight.) Whereas it is tough for humans to calculate this, it is easy for computer programs. It so happens that NSU is a game where a single deuce is worth very close to even money so sometimes it is correct to hold the deuce and sometimes it is correct to hold the 4-card straight.
If we hold the one deuce, 4-card flush, however, there are 9 cards that yield 3-of-a-kind, 12 cards that yield a flush, and 26 that yield nothing. The higher pay for flushes means they can overcome a zero score for 24 other cards, but since there are 26 such cards, a 1-deuce 4-card flush is worth less than even money. (If flushes only paid double your money, as they do in many Deuces Wild games, a 1-deuce 4-card flush would be worth about 70% as much as your original bet.)
There is a general principle at work here. On some hands (three of a kind or four of a kind) where whether or not there is a deuce present is irrelevant. That is, the value of 444 is identical to that of W44. On other hands, such as a 4-card flush, a deuce being present adds to the 3-of-a-kind possibilities but doesn't affect the chances for getting a flush itself. (4-card flushes with no deuce and 4-card flushes containing a deuce each have 12 completion cards). But with straights, in addition to adding 3-of-a-kind possibilities, a deuce turns an open-ended straight into a SUPER-open-ended straight. Going from 12 completion cards to 19 is a significant difference.
In conclusion, a 1-deuce 4-card straight has 1.58 times as many cards to complete it than does a 1-deuce 4-card flush. This more than offsets the fact that flushes pay 1.50 times as much. Strange.
Liam W. Daily pointed out this paradox to me. He didn't tell me the answer, but rather challenged me to think about it. He said, "You'll enjoy figuring it out." He was right.
[ learn video poker! ]

